> Energy band gap>
GaAs |
AlxGa1-xAs |
InxGa1-xAs
> Refractive index
> GaAs |
AlAs |
AlxGa1-xAs |
InxGa1-xAs
> Devices
> Bragg mirror |
SAM |
RSAM |
SA |
SANOS |
SOC |
Microchip |
PCA
> Device application
> Papers |
Patents |
FAQs

SA - Saturable Absorber
SA construction and application
Construction:
- The SA consists of a saturable absorber layer on semi-insulating (transparent) GaAs wafer.
- Both sides of the SA are anti-reflection (AR) coated for the laser wavelength.
Behaviour:
- The SA is a nonlinear absorber
- The transmittance increases with increasing pulse energy.
- The typical saturation fluence of a SA is higher then that of a SAM.
- After a relaxation time < 100 ps the SA goes back in the ground state.
Application:
- Using a saturable absorber (SA), a self-starting, passively mode-locked laser with a very stable pulse repetition rate can be realized.
- SAs mainly for fiber laser mode-locking in a wide spectral region from 1030 nm up to 2800 nm wavelength are available.
- A ring laser can be easily realized by using a SA.
- The SA can be used with free-space optics or fiber coupled.
- The heat removal from SA is less efficient then from a SAM.
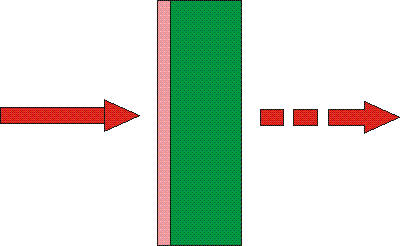
• Absorptance
Absorptance
The absorptance of the SAM consists of two parts:
- saturable absorption As
- non-saturable absorption Ans.
The non-saturable part Ans of the absorption can be caused by macroscopic crystal defects with very short relaxation time
of the excited carriers.
The non-saturable absorption decreases with increasing relaxation time of the excited carriers in the absorber material.
In case of absorbers with a short relaxation time of ~ 1 ps the non-saturable part of the absorption can be
Ans ~ 0.2 · A0.
The total absorption is the sum of both parts A1 = As + Ans.
The saturation of the absorption can be described with the following formula:
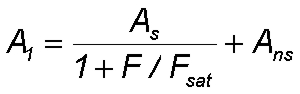
with
- A1 - Sum of saturable and non-saturable absorption
- As - saturable absorption
- Ans - non-saturable absorption
- F - radial dependent pulse fluence
- Fsat - saturation fluence of the absorber.
The pulse fluence F depends on the beam radius r for a Gaussian pulse as follows:
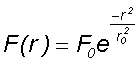
with
- F(r) radial dependent pulse fluence
- F0 - maximum fluence on the beam axis
- r0 - Gaussian beam radius
The fluence and consequently also the saturation depend on the radial distance r from beam axis. To get the effective absorption A for the pulse an averaging over the whole illuminated area on the absorber is needed.
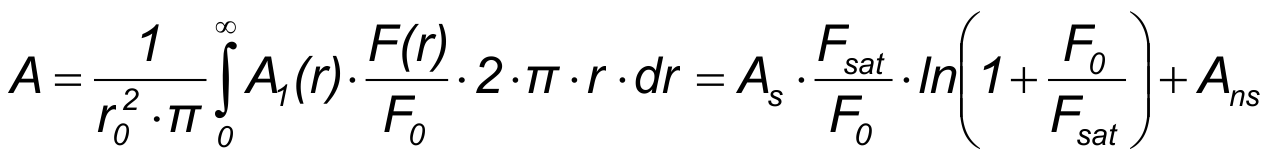
The figures below show the saturation behaviour according to the formulas above for the absorption A1 and the averaged absorption A with a
certain value of non-saturable absorption Ans = 0.1 · A0.
The averaging results in a lower saturation simulating an additional virtual non-saturable absorption.
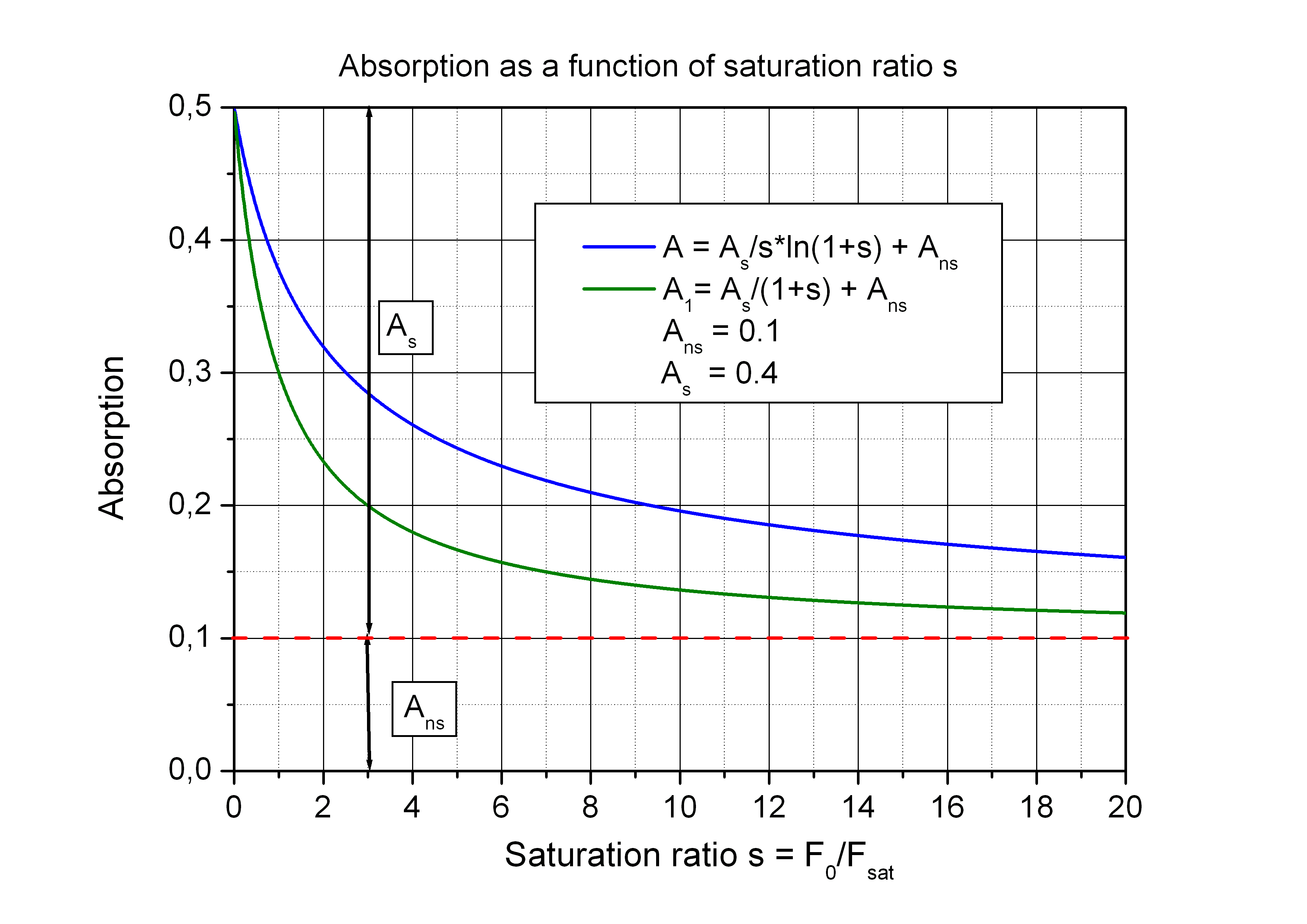
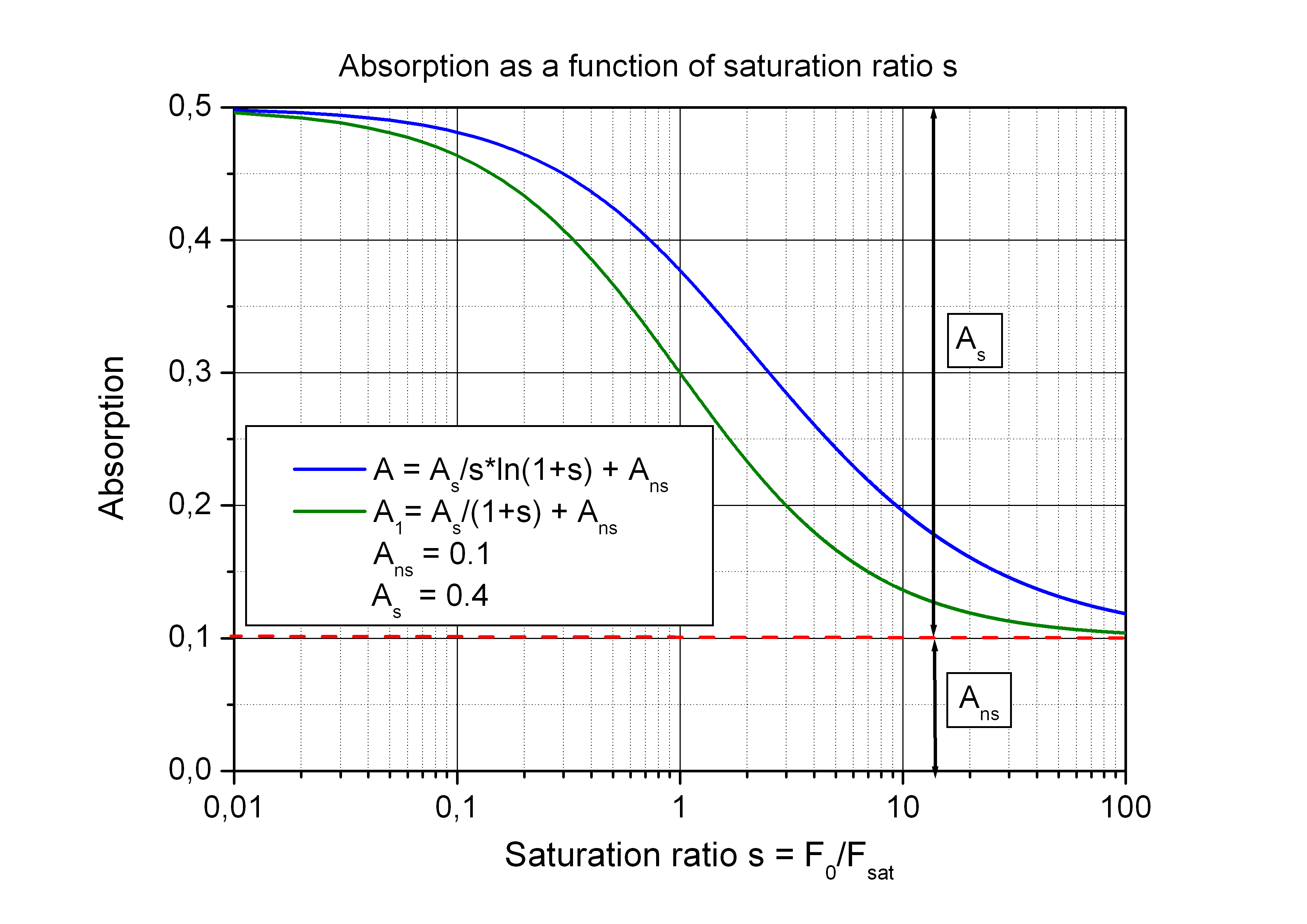
Typical values of a saturable absorber for mode-locking a fiber laser are A ~ 0.3 and Fsat ~ 200 µJ/cm2.
Two photon absorption
For short pulses the two-photon absorption ATPA increases the total absorption as follows:
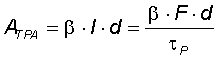
with
- β - two-photon absorption coefficient
- I - pulse intensity
- d - absorber layer thickness
- F - pulse fluence
- τP - pulse duration.
The integration of the time dependent intensity I(t) over the pulse duration τP results in the pulse fluence F. Therefore the pulse fluence can be approximated as F ~ I · τP.
• Relaxation time
Relaxation time τ
The saturable absorber layer consists of a semiconductor material with a direct
band gap slightly smaller than the photon energy of the laser beam. As a result of the photon absorption
electron-hole pairs are created in the absorber film.
For laser mode-lockig the relaxation time τ of the excited carriers shall be
somewhat longer than the pulse duration. In this case the back side of the pulse is still free of absorption, but during the
whole period between two consecutive pulses the absorber is non saturated and serves for a high absorption.
Because the relaxation time due to the spontaneous photon emission in a direct
semiconductor is about 1 ns, some precautions has to be done to shorten it for mode-locking application.
Two technologies are used to introduce lattice defects in the absorber layer for fast non-radiative relaxation of excited carriers:
- low-temperature molecular beam epitaxy (LT-MBE)
- ion implantation.
The parameters to adjust the relaxation time in both technologies are the growth temperature in case of LT-MBE and the ion dose in case of implantation. Typical values of the relaxation time τ of SAs are between 500 fs and 30 ps.
• Saturation fluence
Saturation fluence Fsat
The saturation fluence Fsat depends on the semiconductor material and the
thickness of the absorber layer. Low saturation fluence has the advantage that the laser mode-locking
can be started at low power level. This avoids a fast absorber degradation
To decrease the saturation fluence, the thickness of the semiconductor absorber layer
is reduced below ~ 10 nm. In this case a quantization of the electron energy and the momentum
in the direction perpendicular to the absorber layer takes place and as a consequence the
density of states decreases below the value of a compact semiconductor. Therefore the absorber layers
in a SA are thin quantum wells with a smaller band gap than the barriers on both sides. If a
larger absorption value of the SA is needed, the number of the quantum wells is increased instead of
using a single thick absorber layer.
Typical saturation fluence of a SA is Fsat ~ 200 µJ/cm² = 0.2 J/m².
• Influence of absorber temperature
Influence of absorber temperature
The imaginary part k of the refractive index and consequently the absorption of a direct semiconductor increases with temperature.
This is also a consequence of decreasing band gap with increasing temperature.
For a typical SA the temperature coefficient of the imaginary part k of the refractive index is
αk ~ 6·10-3/K.
With this coefficent the temperature dependent value for k can be calculated by
k(T) = k(T0)·(1+αk·ΔT)
Therefore k and also the SA absorption increase by 50 % if the absorber temperature increases by 83 K. This temperature dependence has a significant influence on laser mode-locking.